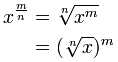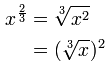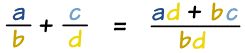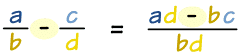Definite Integrals

Integration

Integration can be used to find areas, volumes, central points and many useful things. But it is often used to find the area under the graph of a function like this: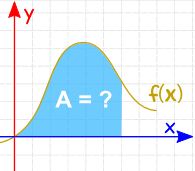
The area can be found by adding slices that approach zero in width: And there are Rules of Integration that help us get the answer.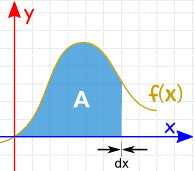

Notation

The symbol for "Integral" is a stylish "S" (for "Sum", the idea of summing slices):

After the Integral Symbol we put the function we want to find the integral of (called the Integrand),

and then finish with dx to mean the slices go in the x direction (and approach zero in width).

Definite Integral

A Definite Integral has start and end values: in other words there is an interval [a, b].

a and b (called limits, bounds or boundaries) are put at the bottom and top of the "S", like this:

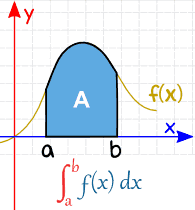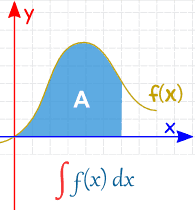Definite Integral (from a to b)		Indefinite Integral (no specific values)

Derivative Rules

The Derivative tells us the slope of a function at any point.

There are rules we can follow to find many derivatives.

For example:

• The slope of a constant value (like 3) is always 0
• The slope of a line like 2x is 2, or 3x is 3 etc
• and so on.

Here are useful rules to help you work out the derivatives of many functions (with examples below). Note: the little mark ’ means "Derivative of", and f and g are functions.

Common Functions	Function	Derivative
Constant	c	0
Line	x	1
	ax	a
Square	x2	2x
Square Root	√x	(½)x-½
Exponential	ex	ex
	ax	ln(a) ax
Logarithms	ln(x)	1/x
	loga(x)	1 / (x ln(a))
Trigonometry (x is in radians)	sin(x)	cos(x)
	cos(x)	−sin(x)
	tan(x)	sec2(x)
Inverse Trigonometry	sin-1(x)	1/√(1−x2)
	cos-1(x)	−1/√(1−x2)
	tan-1(x)	1/(1+x2)
Rules	Function	Derivative
Multiplication by constant	cf	cf’
Power Rule	xn	nxn−1
Sum Rule	f + g	f’ + g’
Difference Rule	f - g	f’ − g’
Product Rule	fg	f g’ + f’ g
Quotient Rule	f/g	(f’ g − g’ f )/g2
Reciprocal Rule	1/f	−f’/f2
Chain Rule (as "Composition of Functions")	f º g	(f’ º g) × g’
Chain Rule (using ’ )	f(g(x))	f’(g(x))g’(x)
Chain Rule (using ddx )	dydx = dydududx

Integration Rules

Integration Integration can be used to find areas, volumes, central points and many useful things. But it is often used to find the area underneath the graph of a function like this:

The integral of many functions are well known, and there are useful rules to work out the integral of more complicated functions, many of which are shown here.

There are examples below to help you.

Common Functions	Function	Integral
Constant	∫a dx	ax + C
Variable	∫x dx	x2/2 + C
Square	∫x2 dx	x3/3 + C
Reciprocal	∫(1/x) dx	ln|x| + C
Exponential	∫ex dx	ex + C
	∫ax dx	ax/ln(a) + C
	∫ln(x) dx	x ln(x) − x + C
Trigonometry (x in radians)	∫cos(x) dx	sin(x) + C
	∫sin(x) dx	-cos(x) + C
	∫sec2(x) dx	tan(x) + C
Rules	Function	Integral
Multiplication by constant	∫cf(x) dx	c∫f(x) dx
Power Rule (n≠-1)	∫xn dx	xn+1n+1 + C
Sum Rule	∫(f + g) dx	∫f dx + ∫g dx
Difference Rule	∫(f - g) dx	∫f dx - ∫g dx
Integration by Parts	See Integration by Parts
Substitution Rule	See Integration by Substitution

Squares and Odd Numbers

Add up odd numbers from 1 onwards and you get square numbers!

• 1 is a square number (= 1 × 1)
• 1 + 3 = 4, and 4 is a square number (= 2 × 2)
• 1 + 3 + 5 = 9, and 9 is a square number (= 3 × 3)
• etc!

Like this:

Odd Number	Running Total
1	1	= 1 × 1
3	4	= 2 × 2
5	9	= 3 ×3
7	16	= 4 × 4
9	25	= 5 × 5
11	36	= 6 × 6
etc...

Is this some kind of magic?

Not really, just look at this picture:

• 1 is a square (a 1×1 square)
• Add 3 and you get a 2×2 square
• Add 5 and you get a 3×3 square
• etc

It is good to know this, as it may help you solve things one day.

Cardinal, Ordinal and Nominal Numbers

Cardinal Numbers

A Cardinal Number says how many of something there are, such as one, two, three, four, five.

A Cardinal Number answers the question "How Many?"

It does not have fractions or decimals, it is only used for counting.

How to remember: "Cardinal is Counting"

Ordinal Numbers

An Ordinal Number tells us the position of something in a list.

1st, 2nd, 3rd, 4th, 5th and so on (seeCardinal and Ordinal Numbers Chart for more.)

How to remember: "Ordinal says what Order things are in".

Nominal Numbers

A Nominal Number is a number used only as a name, or to identify something (not as an actual value or position)

How to remember: "Nominal is a Name".

Ratio - Make Some Chocolate Crispies

To make these chocolate crispies I used: 20 g (grams) of chocolate 15 g of cornflakes or similar This made 1 cake. Recipe Here

Your mathematics task is to: 1) calculate the ratio of chocolate to cornflakes, and then: 2) work out the amount of ingredients to make 21 cakes.

1) We can see that the ratio of chocolate to cornflakes is 20:15

But this can be simplified further. The Greatest Common Factor is 5, so:

If we have 20 parts chocolate to 15 parts cornflake, divide each side by 5 and we get 4:3

This is the ratio of chocolate to cornflakes.

2) We need to work out how much chocolate and cornflakes we need to make 21 cakes.

The recipe is for 1 cake but we want 21, so multiply both ingredients by (21 cakes / 1 cake), or simply by 21:

• 21×20 = 420
• 21×15 = 315

So to make our 21 cakes we need:

• 420 g of chocolate
• 315 g of cornflakes

Supplementary Angles

Two Angles are Supplementary when they add up to 180 degrees.

These two angles (140° and 40°) are Supplementary Angles, because they add up to 180°:

Notice that together they make a straight angle.

But the angles don't have to be together.

These two are supplementary because
60° + 120° = 180°

Complementary vs Supplementary

A related idea is Complementary Angles, they add up to 90°

How to remember which is which? Easy! Think:

• "C" of Complementary stands for "Corner"  (a Right Angle), and
• "S" of Supplementary stands for "Straight" (180 degrees is a straight line)

You can also think "Supplement" (like a Vitamin Supplement) is something extra, so it is bigger.

Laws of Exponents

Laws of Exponents

Law	Example
x1 = x	61 = 6
x0 = 1	70 = 1
x-1 = 1/x	4-1 = 1/4
xmxn = xm+n	x2x3 = x2+3 = x5
xm/xn = xm-n	x6/x2 = x6-2 = x4
(xm)n = xmn	(x2)3 = x2×3 = x6
(xy)n = xnyn	(xy)3 = x3y3
(x/y)n = xn/yn	(x/y)2 = x2 / y2
x-n = 1/xn	x-3 = 1/x3
And the law about Fractional Exponents:

Fractions in Algebra

We can add, subtract, multiply and divide fractions in algebra in the same way we do in simple arithmetic.

Adding Fractions

To add fractions there is a simple rule:

Example:

x2 + y5 = (x)(5) + (2)(y)(2)(5)

= 5x+2y10

Subtracting Fractions

Subtracting fractions is very similar, except that the + is now −

Example:

x + 2x  −  xx − 2  =  (x+2)(x−2) − (x)(x)x(x−2)  

=  (x² − 2²) − x²x² − 2x

=  −4x² − 2x

Common Big and Small Numbers

Common Big and Small Numbers

Name	The Number	Prefix	Symbol
trillion	1,000,000,000,000	tera	T
billion	1,000,000,000	giga	G
million	1,000,000	mega	M
thousand	1,000	kilo	k
hundred	100	hecto	h
ten	10	deka	da
unit	1
tenth	0.1	deci	d
hundredth	0.01	centi	c
thousandth	0.001	milli	m
millionth	0.000 001	micro	µ
billionth	0.000 000 001	nano	n
trillionth	0.000 000 000 001	pico	p

Area of Plane Shapes

	Triangle Area = ½ × b × h b = base h = vertical height			Square Area = a2 a = length of side
	Rectangle Area = w × h w = width h = height			Parallelogram Area = b × h b = base h = vertical height
	Trapezoid (US) Trapezium (UK) Area = ½(a+b) × h h = vertical height			Circle Area = π × r2 Circumference = 2 × π × r r = radius
	Ellipse Area = πab			Sector Area = ½ × r2 × θ r = radius θ = angle in radians